Wombat2 is the new name, returning to https://wombatlang.blogspot.com/

 I've decided to bring back the wombat name. Except that it is now wombat2 - no space before the 2. This will hopefully be easier to search for.

Future posts back at https://wombatlang.blogspot.com/.

Also: I've started posting videos on my PLodicy youtube channel: https://www.youtube.com/@RobertSmart/.

The Ken Type System (Draft 1)

The Ken Type System (Draft 1)

Values have a type. Types are in indexed families which have a base and an index type. The base is an EmbedProc (a total, 1-1 procedure that has an inverse) from the index type to Type. So we can get the index value by running the inverse of the base's EmbedProc.

At run time we need to keep the value, and the index value. But the index value is also, in general, of an indexed type. So we also need its index, and so on. This must terminate with a simple unindexed type.

Ken is an expression language. There isn't a division between statements and expressions, just expressions within expressions. An important subset of expressions are Terms. A constant or variable is a Term. The application of a pure total procedure to a Term is a Term. A tuple of Terms is a Term. These simple well-behaved expressions are important for various things.

In particular the expression for the index of a type must be a Term. So an expression for a type is a term. Every expression at compile time has a Type term. This might have an index which is a value with a type, and so on. This is the Type the expression will have if it doesn't fail. Expressions that always fail are a compile error.

Stages of Typing

At compilation time we translate the source into an AST (Abstract Syntax Tree). This is just an expression with inner expressions. Every expression has a type with a known base and an index which is a term. The index then has its type, and so on.

Execution creates an Execution Tree (ET). In particular, when a closure is called, that sticks a copy of the closure's inner expression in the ET, with the parameter filled in. This, like every expression, starts with an elaboration-time type, which gets refined during execution. Execution in Ken is just about reducing the execution-time type of every expression to satisfy the needs of effects (such as interaction with the outside world).

Commonly expressions reduce to values. The type of a value is some general type restricted to the specific value. Expressions can also fail when they are restricted to the empty set of values.

Equality

For any type X, there is a type representing equality for that type. Eq%(X)(x1,x2) is a type that is empty if x1 and x2 are not equal. If the type has a value then it is a proof or witness that x1 and x2 are equal.

But since Eq%(X)(x1,x2) is a type, then it must also have a type representing equality of its values. This is handled in Ken by having an additional optional Nat parameter representing depth. So Eq%(X) is the same as Eq%(X,0), and Eq%(X,n+1) is the same as Eq%(Eq%(X,n)).

There is also a type Neq%(X)(x1,x2), which equals Not%(Eq%(X)(x1,x2)), a value of which is a witness that x1 and x2 are not equal. Most types conform to the Distinguishable behaviour which allows one to easily get a witness of one or the other, in the form of a value of type:

DisjointUnion( .eq->Eq%(X)(x1,x2), .neq->Neq%(X)(x1,x2) ).

Subtypes of Types

A PropType is one which has at most one value, and its equality type is also a PropType (so that all levels of equality have at most one value). These types are used for propositions.

A SetType is one whose equality type is a PropType. All common types are of this form.

Behaviours and Properties

Values generated by Terms can have properties. These are just values of some other type, but they can be dependent on free identifiers in the Term. Most importantly this includes types, and the properties of types are a key feature of the Type System.

Properties originate in Behaviours (spelt with or without the "u"). Values of any type can have properties and can conform to Behaviours, but we are interested in Behaviours of types. A Behaviour is created with the behaviour operator:

behaviour of X extends <an X Behaviour> by <an X=>Type procedure> 

The extends subopertor is optional. Here is the Semigroup behaviour:

    `Semigroup = #  backtick, `, prefix means this is a new name not some outer name
       behaviour of Type by
           {' Type>:`T => Type : # note X:>x is the same as x:X, but returns X not x.
               ['  `op: T*T=>T; # NB. T*T=Tuple[T,T]
                   `associative:
                       ∀%{' T:>`u * T:>`v * T:>`w => Type :
                            Eq%(T)(op(op(u,v),w),op(u,op(v,w)))
                         };
               ]
           }

The type returned by that procedure parameter (from [' to ]) is a Structure which specifies the properties, in this case op and associative, and their respective types. We see that associative has a complex type, as is common for proposition types. We declare that a type conforms to a Behaviour with a conformsTo operator:

Nat conformsTo Semigroup by
   @Semigroup(Nat)[' op=add; associative=...; ]

This bestows the .add and .associative properties on Nat.

The way this typically is used in Ken is to provide the interpretation of  operators. So, x+y can map to @Monoid(Union(TypeOf(x),TypeOf(y))).op(x,y). The equality type operator is ==%, and x==%y maps to Eq%(Intersection(TypeOf(x),TypeOf(y)))(x,y).

More detail on this in the later section on the lattice of types.

As with types, behaviours can come in indexed families. For example Nat is a semigroup with addition, but also with multiplication, maximum, and very many less interesting ones. So Semigroup might instead be an Atom<=>Behaviour, and our example above would then be Semigroup.add.

Creating Types and Behaviours

Types have an associated Behaviour used to handle values of that type. Types arise in the folllowing ways:

• Built in types;
• Primitive types;
• Types defined uniquely by Behaviour;
• Types defined by a Behaviour plus a default implementation.

Ideally every operation is based on properties of the types of the entities involved. Operations can also be done by converting to and/or from an implementation. Any procedure that uses this is "Evil" unless there is a proof that equal inputs yield equal outputs. However if the mapping procedure from a type to its implementation is 1-1 then that procedure with its inverse can be added to the type's properties. Consider Rational numbers. An obvious implementation is as 2 integers, with a/b = c/d iff ad=bc. This allows equal Rationals to map to unequal pairs. If, instead, our implementation is as an integer and a relatively prime natural number greater than 0 (i.e. GCD of 1), then the mapping is 1-1 and this embedding is also a valid property.

Primitive types are unindexed types representing the values supported by the compiler target, whose properties are the only ways to use values of the type. One target is the compiler's provided scripting language. If this is different from the target language for run time execution then at elaboration time, constructing the execution tree, compile-time values get converted to run-time values.

The classic example of a type defined by its behaviour is Nat, the natural numbers. This has 4 properties: zero:Nat, succ:Nat<=>Nat, succNotZero and induct. The latter 2 are more complex universally qualified proposition types. However definitional types can be much simpler, as mentioned above with Rational numbers defined by the 1-1 mapping to an Integer*Nat1 pair with GCD of 1. For these types defined by behaviour we provide a mapping between 2 arbitrary implementations, using the properties to construct the mapping, plus the invertible maps to the implementing types. At least one implementation needs to be provided, including a proved construction of the behaviour's properties.

Where the types behaviour is not enough to uniquely define the type, then a default implementation is required and other implementations must provide conversion to and from the default one.

More detail in Appendix A, but here are types that are relevant to the following discussion:

• Type and Behaviour are types. They technically exist in a higher Universe, but have shadows in the base universe that satisfy runtime uses.
• Nat : natural numbers from 0. There is also Nat1 starting at 1.
• Atom : constants are a dot followed by an identifier.
• String : of characters. A constant is in "s with a \ escape.
• Proc(X,Y) : pure dependent procedures from X to Y that can fail. And many variants: TProc is total, EmbedProc is 1-1 invertible, ... Also Evil variants, discussed later.
• Effect(X,Y) : Like a Proc but with time dependent semantics. Similar variants.
• Expression, Term, Closure : allow some introspection.
• Tuple[X,Y,...] : dependent on a List(Type). Values created by comma operator.
• Multiset(X) :  (aka Bag(X)) a set with repetitions allowed -- i.e. not ordered and no attempt to find and remove duplicates.
• Set(X): As for Bag, but no duplicates. I.e. we need a witness for Neq% for each pair.
• Structure(Term) : [' <term> ], see later section.
• UnionType(Set(Type)) where the Set(Type) is restricted to have no UnionType and no Type that is lower than another (so an antichain). The procedure Union:Bag(Type)=>Type creates the UnionType by expanding inner Unions and removing any types lower than or equal to another.
• Similarly IntersectionType and Intersection procedure. We have to keep Unions in our antichain to keep properties that are in all those of the Union.
• Many types representing propositions.
• ...

The Lattice of Types

We create a partial order of types by isA declarations, which have this form:

X isA Y by <an EmbedProc from X to Y>

As the name suggests, this is intended to provide a form of subtyping.

• The expression returns a value (witness) of the proposition type IsA%(X,Y).
• Cycles are not permitted, so this extends to a partial order (by transitive closure).
• We then extend this to an order lattice by creating Union and Intersection types.

• If X isA Y then Union(X,Y) is Y and Intersection(X,Y) is X.
• Union(X,Union(Y,Z)) is the same as Union(X,Y,Z).
• Ultimately there is one Union type for any Bag(Type) with no Unions and no types below another in the Bag. But we keep Intersections.
• Similarly for Intersections we eliminate types above and any Intersections, but keep Unions.

While all properties come from Behaviours, types also inherit properties from types above them. Note that they don't inherit Behaviours, only individual properties. If they already have that property (with the same Behaviour and the same property name), or they inherit it more than once from above, then those properties are required to be compatible. This is described in Appendix B. Equality is the best sort of compatibility, but checking compatible behaviour can also be deferred.

In the hierarchy the conversions up are 1-1 and always succeed, and conversions down fail if the upper value does not correspond to a lower value. Suppose we have the following seven types with the obvious isA relationship given by up arrows:

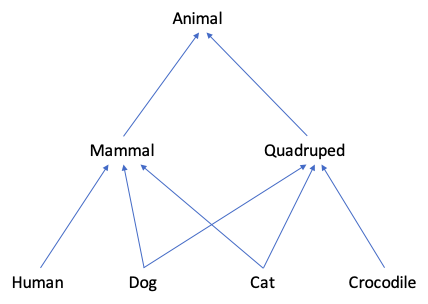
The coherence requirement says a Dog must end up as the same Animal whichever route it takes upward.

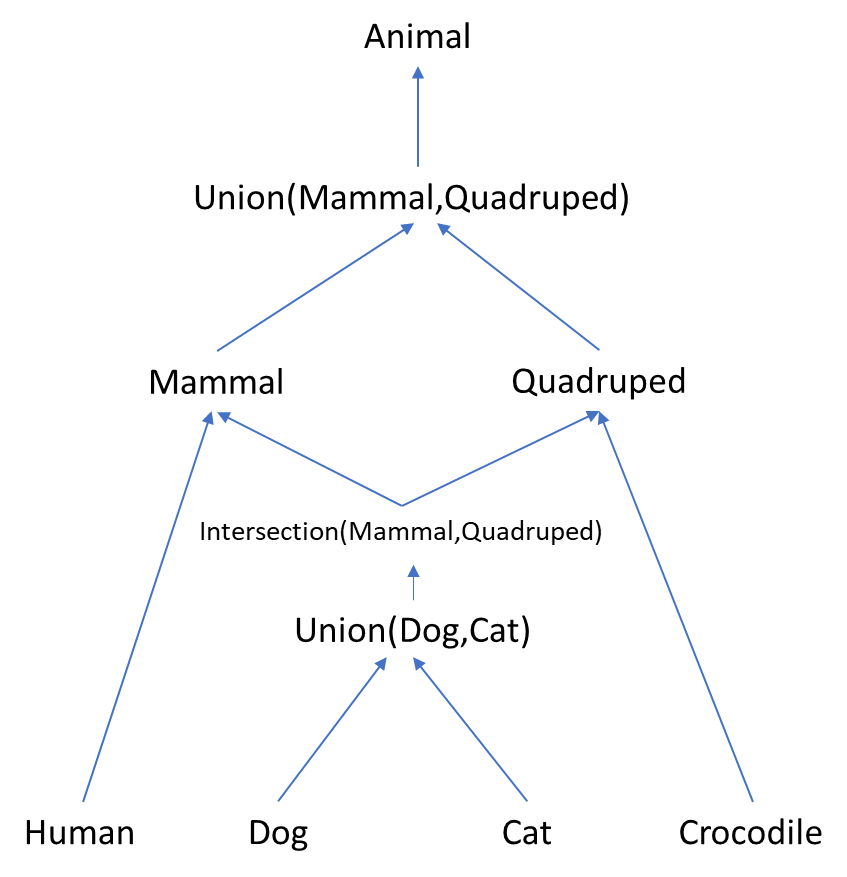
Values in the Union of Mammal and Quadruped will be either one or the other, with an indicator of which. The values in Intersection are those of the Union of all types that are below both. The equality type on a Union has the effect that two values are equal if they come from the same value in the Intersection even if they come up by different routes.

Intersection(Mammal,Quadruped) has the same values as Union(Dog,Cat), but it only has the properties from Mammal and Quadruped, while the Union can have other properties if Dog and Cat have additional isA relations beyond those shown. So our lattice of types has a perfect duality between values and properties, with values increasing and properties decreasing as you go up. Type Any at the top has all values and type Empty at the bottom has all properties.

We need to define the upward (isA) link from the Union to Animal. We have to go down before up:

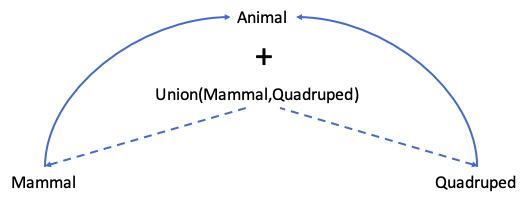
The defining property of Union means that one or both of the down links must succeed. The uplinks then combine with a switch statement as described later on. The Union inherits all the properties of Animal, but has lost all other properties of Mammal and Quadruped. How this works will become clear with a numerical example.

Taking the meet and join of the empty collection of types we get the type Empty = Union() and Any = Intersection().

In the following, complex integers are also known as Gaussian integers, similarly for rational. There are, of course, isA links not shown from Rational up, and from ComplexInt up to ComplexRational.

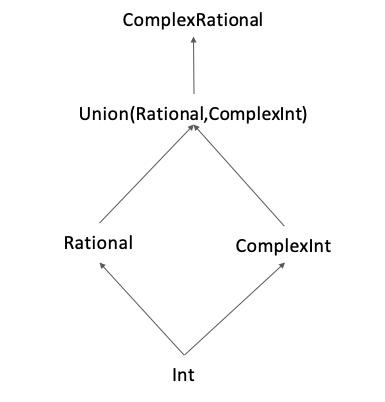
Suppose that the 4 numeric types have the same .add property, in the sense that it comes from the same Behaviour. These procedures have type TProc(T*T,T) for each type T. They are required to be compatible in the following sense: The lower types can also run the .add procedures inherited from above and they must combine correctly in a sense described more fully later. Properties must either be the same or at least behave compatibly.

Because the Union is below ComplexRational, it inherits that .add which is a procedure taking two ComplexRationals and returning a ComplexRational result. So if you try to use that .add on a pair of values from the Union then those values will convert to ComplexRational and give a ComplexRational result, as one might expect. Indeed due to the induced isA relations on a tuple with a Rational and a ComplexInt, if you try to add a Rational to a ComplexInt you get a ComplexRational result, as you or I would if working on paper.

Subset Types

Given a type T, and a proposition type P(t) indexed by (dependent on) T, then we can define a subset type T/P consisting of those values of t:T for which P(t) is non-empty. For example the natural numbers greater than 7 are Nat/{Nat<=>Type: $ >% 7 }.

Subset types get all their properties from their parent. The only direct isA relations allowed are with the parent and other subset types of the same parent. T/P isA T/Q when: forall% t:T ( P(t) implies% Q(t)) is nonempty.

Example Applications

As mentioned earlier, operators commonly map to procedures which use the hierarchy to do the right thing with values of different types: When this is combined with the automatic conversions to and from subtypes, everything just works in a way that is very close to the way dynamic typing works in languages such as Python. So, x+y maps to @Monoid(Union(TypeOf(x),TypeOf(y))).op(x,y). The equality type operator is ==%, and x==%y maps to Eq%(Intersection(TypeOf(x),TypeOf(y)))(x,y).

For proposition types, the "isA" relation is the same as "implies". So, for example, we have X isA (X Or% Y). But we see that X or Y is true iff Union(X,Y) is not empty. And indeed in Ken X Or% Y is Union(X,Y). We also have that for all types X and Y: (X And% Y) isA X and also isA Y. So conveniently in Ken, X And% Y is Intersection(X,Y). It is true that Tuple[X,Y] is non-empty iff X and Y are both non-empty, but Intersection is more natural since it corresponds to the matching Venn diagram.

The most important application is at execution time, or when doing symbolic execution with terms at compile time. Expressions, and particularly propositional expressions such as equality, act as constraints. Execution consists of moving the known type of an expression down in the hierarchy. In general it reduces to a type restricted to a single value.

---

Appendix A: Details of Types and Behaviours

TBS

Appendix B: Details of Case, Combine and Compatible

TBS

Followup to my Stackexchange question

I posted a question on Stackexchange long ago about Ken's type system. I tried to write a comment about how I resolved the question, but my answer was too long for a comment, so I'm putting it here.

While not of general interest, let me mention how this turned out. The type system for my programming language has a builtin hierarchy that is effectively subtyping. Types have values and properties. A 1-1 embedding means that the values of a type can be regarded as being in one above. Also types inherit all the properties of types above. So if Integer is below Rational then Integer also has the "denominator" property. There are coherence constraints. As we go up the hierarchy we get more values and less properties. "Any" at the top has all values and "Empty" at the bottom has all properties.

The way I add Union and Intersection types is not completely free because there is the additional constraint that types are equal if they have the same values and properties.

Union of types is just values of those types with a memory of which they came from, but two values are equal if they are equal in the Intersection of the two types they came from (so an Integer in the Union of Rational with GaussianInteger is the same whichever route it takes upward). The properties of the Union are those that are from all types that are above every type in the Union. (this is "parametricity" when that is just Any).

To get the intersection of a set of types: the properties are just those of any of the types. The values are from the Union of all the subtypes that are below every type (but that Union type can have more properties, so it is exactly below the Intersection).

We don't get more types by considering Unions or Intersections which have Union or Intersection arguments, so that's it.

Is this mathematically sound or implementable? Time will tell, I hope. If anyone is interested in the gory details, this blog post has the link: https://ken-lang.blogspot.com/2023/06/ken-has-spec.html.

At some point John Baez got involved, and in the midst of some helpful comments he said that non-bounded lattices were relatively unimportant. and when he said just "lattice" he meant a bounded lattice. Mathematics needs an IMU, like Astronomy's IAU, to define standard definitions and notation.

The Verse Programming Language

 If you've seen this video on the Verse language:

then you might have seen quite a few bits that are similar to Ken. Examples include bidirectional execution (when possible), the way failure corresponds to zero possible values. Was I influenced by Verse?

Well no, though I might be in future. However the stuff where they are similar was already in the Wombat Programming Language. I gave a talk about it in Wellington at a side-meeting to the Asian Programming Languages and Systems meeting in 2018. I like to imagine that I influenced somebody there and that influence found its way into Verse. However more likely these are just ideas whose time has come. For bidirectional execution I was certainly influenced by Mercury, which is an Australian language related to Prolog, and the video mentions being influenced by Prolog.

Trivia

Ken's mascot is Kenny the wombat.

Ken's motto is "Stop messing about": https://youtu.be/3W4UkoJ3-zA?t=28.

I just need an AI expert to make a video of a wombat saying "stop messing about" in Kenneth William's voice.

Ken has a spec

 I finally have a spec for the Ken Programming Language that I'm happy with. It is at https://docs.google.com/document/d/1EPYLojn9PzslmOFhBT4PYFKFGkrmreRBxPHN_KHEkRw/edit?usp=sharing. It's a bit over-mathematical. Don't let that fool you. It is meant for general programming, but with a lot of mathematics made available with proofs.

[Update 2023-06-08: It seems there was a comment in the doc, but I didn't see it and somehow lost it. Obviously I don't understand it, so I'm turning it off. Big apologies if I lost your comment. Feel free to comment here or email me at robert.kenneth.smart@gmail.com.] Comments are enabled in the doc, or comment here.

This is a successor to the wombat programming language: https://wombatlang.blogspot.com/. There is an implementation of wombat at https://github.com/rks987/marsupial that does just enough for the talk I gave on it. I am adding Python types to parts of that code which I plan to use for Ken.

I'm happy to give talks on the Ken specification and plans. Suggested talk titles are:

• "Why proposition types improve programming language design" for computer folk.
• "Expressing Category Theory in the Ken Programming Language" for math folk.

Or any other aspects of the language.

I can give in person talks in South East Australia. I have no experience giving remote talks, but at least I've got a reasonable USB microphone.